Multidimensional Gaussian distribution and classification with Gaussians

by Guido Sanguinetti

1-D Gaussian distribution

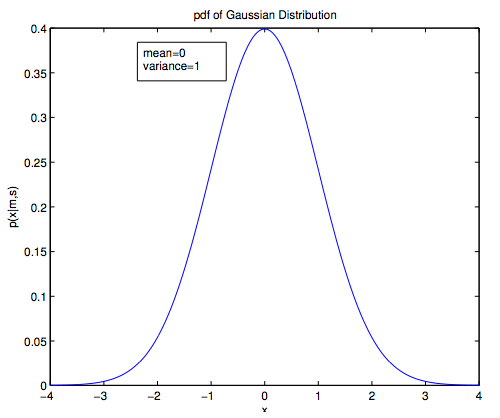
1-D Gaussian with zero mean and unit variance ($\mu = 0$, $\sigma^2 = 1$):

$$\begin{equation} p(x|\mu,\sigma^2)=N(x;\mu,\sigma^2)=\frac{1}{\sqrt{2{\pi}\sigma^2}}{\rm exp}[\frac{-(x-\mu)^2}{2\sigma^2}] \end{equation}$$

The multidimensional Gaussian distribution

• The $d$-dimensional vector $X$ is multivariate Gaussian if it has a probability density function of the following form:¹

$$\begin{equation} p(X|M,\sum)=\frac{1}{(2\pi)^{d/2}|\sum|^{1/2}}{\rm exp}[-\frac{1}{2}(X-M)^{T}{\sum}^{-1}(X-M)] \end{equation}$$

• The pdf is parameterized by the mean vector $M$ and the covariance matrix $\sum$.

• The 1-D Gaussian is a special case of this pdf.

• The argument to the expontial $0.5(X-M)^T{\sum}^{-1}(X-M)$ is referred to as a quadratic form.

Covariance matrix

• The mean vector $M$ is the expectation of $X$:

$$M = E[X]$$

• The covariance matrix $\sum$ is the expectation of the deviation of $X$ from the mean:

$${\sum} = E[(X-M)(X-M)^T]$$

• ${\sum}$ is a $d \times d$ symmetric matrix:

$$\sum_{ij} = E[(X_i-M_i)(X_j-M_j)]=E[(X_j-M_j)(X_i-M_i)]=\sum_{ji}$$

• The sign of the covariance helps to determine the relationship between two components:
  • If $X_j$ is large when $X_i$ is large, then $(X_j-M_j)(X_i-M_i)$ will tend to be positive;
  • If $X_j$ is small when $X_i$ is large, then $(X_j-M_j)(X_i-M_i)$ will tend to be negative.

The covariance matrix is not scale-independent: Define the correlation coefficient:

$$\rho(X_j,X_k)=\rho_{jk}=\frac{S_{jk}}{\sqrt{S_{jj}S_{kk}}}$$

• Scale-independent (i.e. independent of the measurement units) and location-independent, i.e.:

$$\rho(X_j,X_k)=\rho(aX_j + b,sX_k + t)$$

• The correlation coefficient satisfies $-1 \le \rho \le 1$, and

$$\rho(x+y)=+1~~~~~{\rm if}~y=ax+b,~~a>0\\ \rho(x+y)=-1~~~~~{\rm if}~y=ax+b,~~a<0$$

Parameters estimation

It is possible to show that the mean vector $\widehat{M}$ and covariance matrix $\widehat{\sum}$ that maximize the likelihood of the training data are given by:

$$\widehat{M}=\frac{1}{N}\sum^{N}_{n=1}X^{n}\\ \widehat{\sum}=\frac{1}{N}(X^{n}-\widehat{M})(X^{n}-\widehat{M})^T$$

The mean of the distribution is estimated by the sample mean and the covariance by the sample covariance.\rho

---